Мышление в действии: решение задач (ВВП)
Книга «Введение в психологию»
Авторы: Р.Л. Аткинсон, Р.С. Аткинсон, Э.Е. Смит, Д.Дж. Бем, С. Нолен-Хоэксема
Под общей редакцией В.П. Зинченко
15-е международное издание, Санкт-Петербург, Прайм-Еврознак, 2007.
Статья из главы 9. Мышление и речь
Для многих людей решение задач олицетворяет само мышление. При решении задач мы стремимся к цели, не имея готового средства для ее достижения. Мы должны разбить цель на подцели и, возможно, поделить эти подцели далее, на еще меньшие подцели, пока не дойдем до уровня, на котором мы располагаем необходимыми средствами (Anderson, 1990).
Эти моменты можно проиллюстрировать на примере простой задачи. Предположим, вам надо разгадать незнакомую комбинацию цифрового замка. Вы знаете только то, что в этой комбинации 4 цифры и что, как только вы набираете верную цифру, вы слышите щелчок. Общая цель — найти комбинацию. Вместо того чтобы пробовать 4 цифры в случайном порядке, большинство людей разделяют общую цель на 4 подцели, каждая из которых соответствует нахождению одной из 4 цифр комбинации. Первая подцель — найти первую цифру, и у вас есть способ ее достижения, а именно: поворачивать замок медленно, пока не услышите щелчок. Вторая подцель — найти вторую цифру, и для этого можно использовать ту же самую процедуру, и так далее со всеми остающимися подцелями.
Стратегии разделения цели на подцели — это главный вопрос в изучении решения задач. Другой вопрос в том, как люди мысленно представляют себе задачу, поскольку от этого тоже зависит легкость решения задачи. Оба этих вопроса рассматриваются ниже.
Стратегии решения задач
Многое из того, что мы знаем о стратегиях подразделения целей, восходит к исследованиям Ньюэлла и Саймона (см. напр.: Newell & Simon, 1972). Как правило, эти исследователи просили испытуемых думать вслух в процессе решения трудной задачи; они анализировали вербальные реакции испытуемых на ключевую для данной стратегии информацию. Ими был выявлен ряд стратегий общего назначения.
Одна стратегия состоит в сокращении разрыва между текущим состоянием проблемной ситуации и целевым ее состоянием, в котором достигается решение. Рассмотрим снова задачу с комбинацией цифрового замка. Вначале наше текущее состояние не содержит знания ни об одной из цифр, а целевое состояние включает знание всех цифр. Следовательно, мы устанавливаем подцель, уменьшая разрыв между этими двумя состояниями; определение первой цифры реализует эту подцель. Теперь текущее состояние включает знание первой цифры. Разрыв между текущим и целевым состоянием все еще существует, и его можно уменьшить, определив вторую цифру, и т. д. Итак, главная идея сокращения разрыва состоит в установлении подцелей, достижение каждой из которых переводит нас в состояние, более близкое к нашей цели.
Сходная, но более сложная стратегия называется «анализ средства и результата». В ней текущее состояние сравнивается с целевым состоянием, чтобы найти наиболее важное различие между' ними; устранение этого различия становится главной подцелью. Затем ведется поиск средства или процедуры для достижения этой подцели. Если такая процедура найдена, но оказывается, что что-то в текущем состоянии не дает ее применить, вводится новая подцель по устранению этого препятствия. Эта стратегия применяется во многих случаях решения задач на основе здравого смысла. Вот пример:
Я хочу отвести своего сына в детский сад. Каковы [наиболее важные] различия между тем, что я имею, и тем, что хочу? Одно из них — расстояние. Что [какая процедура] изменяет расстояние? Мой автомобиль. Мой автомобиль не работает. Что нужно, чтобы он заработал? Новый аккумулятор. Где есть новый аккумулятор? В автомастерской.
(Newell & Simon, 1972; цит. по: Anderson, 1990, р. 232).
Анализ средства и результата — более сложная стратегия по сравнению с сокращением разрыва, поскольку он позволяет предпринять действие, даже если оно приводит ко временному уменьшению сходства между текущим и целевым состоянием. В вышеприведенном примере автомастерская может находиться в противоположном направлении от детского сада. Так что, отправляясь в мастерскую, вы тем самым временно увеличиваете расстояние до цели, и все же этот шаг существен для решения задачи.
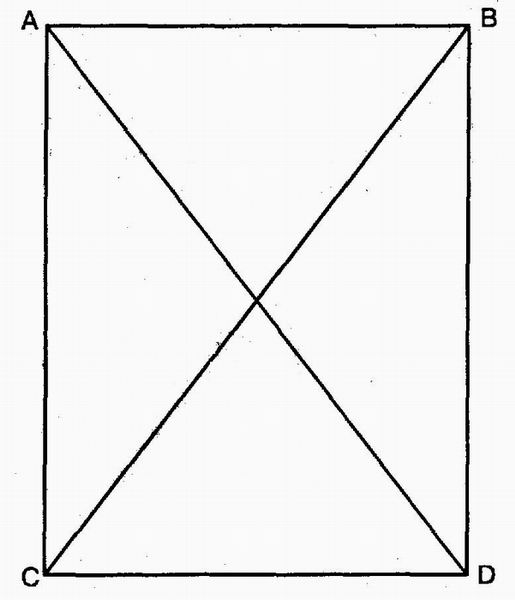
Еще одна стратегия — это действие, в котором происходит обратное движение от цели. Она особенно полезна при решении математических задач, пример одной из которых показан на рис. 9.12. Задача такая: зная, что ABCD — прямоугольник, доказать, что диагонали AD и ВС равны. Мысленно двигаясь назад, можно рассуждать так:
Как доказать, что AD и ВС равны? Я мог бы это сделать, если бы доказал, что треугольники ACD и BDC равны. Я могу доказать, что треугольники ACD и BDC равны, если докажу, что две стороны к заключенный между ними угол равны.
(взято из: Anderson, 1990, р. 238).
Мы рассуждаем, идя от цели к подцели (доказывая равенство треугольников), от этой подцели — к другой подцели (доказывая, что стороны и угол равны) и т. д., пока мы не подойдем к подцели, для реализации которой у нас есть готовое средство.
Три рассмотренные нами стратегии — сокращение разрыва, анализ средства и результата и движение от цели — являются чрезвычайно общими и могут применяться практически к любой задаче. Эти стратегии, которые часто называют слабыми методами, не основываются ни на каком конкретном знании и могут быть даже врожденными. Люди могут особенно полагаться на эти слабые методы, когда они впервые изучают какую-либо область и работают над задачами с незнакомым содержанием. Kale мы скоро убедимся, когда люди получают специальные знания в какой-либо области, они разрабатывают более мощные предметно-ориентированные методы (и репрезентации), которые начинают преобладать над слабыми методами (Anderson, 1987).
Представление о задаче
Способность решить задачу зависит не только от стратегии ее декомпозиции, но также и от того, как мы её себе представляем. Иногда лучшим оказывается представление в форме высказываний (пропозициональная репрезентация); в других случаях более эффективным будет зрительное представление, или образ. Для иллюстрации рассмотрим следующую задачу:
Однажды утром, на рассвете, монах стал взбираться на гору. Узкий проход шириной один или два фута спиралью обвивал гору, ведя к храму на вершине. Монах взбирался с разной скоростью, часто прерывая путь для отдыха. Он добрался до храма незадолго перед закатом. Проведя несколько дней в храме, он начал свой путь назад по тому же пути, выйдя на рассвете, и снова шел с разной скоростью со многими остановками в пути. Его средняя скорость спуска была, конечно, больше средней скорости взбирания на гору. Докажите, что на пути существует определенное место, в котором монах находился по пути вперед и назад точно в одно и то же время дня (Adams, 1974, р. 4).
Пытаясь решить эту задачу, многие люди начинают с пропозициональной репрезентации. Они могут даже пытаться выписать ряд уравнений и вскоре запутываются. Эту задачу гораздо легче решить, если представлять ее зрительно. Все, что надо сделать, — это представить мысленно, как путь монаха вверх накладывается на его путь вниз. Вообразите одного монаха, идущего снизу, а другого — идущего сверху. Независимо от того, какая у них скорость, в некоторый момент времени и в некотором месте пути они должны встретиться. Поэтому должно существовать место на пути, которое монах занимал в обоих путешествиях в то же самое время дня (заметьте, что в задаче не спрашивается, где находится это место).
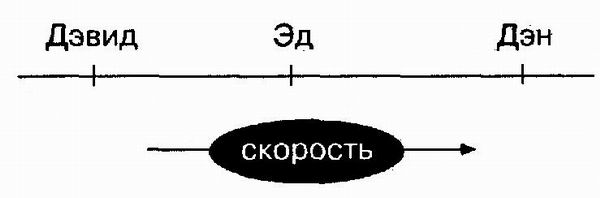
Некоторые задачи легко решаются путем манипулирования высказываниями либо образами. Это можно показать на следующей простой задаче: «Эд бегает быстрее Дэвида, но медленнее Дэна; кто из троих самый медленный? » Чтобы решить эту задачу при помощи высказываний; заметим, что первую часть этой задачи можно представить в виде высказывания, в котором «Дэвид» — это субъект, а «медленнее, чем Эд» — предикат. Вторую часть, за дачи можно представить в виде высказывания, в котором «Эд» — субъект, а «медленнее Дэна» — предикат. Затем можно вывести, что Дэвид медленнее Дэна, откуда следует, что самый медленный — Дэвид. Чтобы решить эту задачу через образы, можно, например, вообразить скорости этих трех человек в виде трех точек на линии:
Затем можно просто считать ответ на вопрос непосредственно из образа. Очевидно, что некоторые люди предпочитают представлять такие задачи в виде высказываний, а некоторые — зрительно (Johnson-Laird, 1985).
Помимо представления задачи на языке высказываний либо образов существует вопрос о том, что представлять. Зачастую трудности с задачами возникают потому, что нам не удается включить в свою репрезентацию задачи какой-либо решающий фактор, или потому, что мы включили в нее что-то, что не является существенной частью задачи. Это можно проиллюстрировать в эксперименте. Одной группе испытуемых дали задачу закрепить свечку на двери, дав только материалы, показанные на рис. 9.13. Решение заключалось в том, чтобы прикрепить коробок к двери кнопкой и использовать его как подставку для свечки. Большинству испытуемых было трудно ее решить, видимо, потому, что они представляли себе коробку как емкость, а не как подставку. Другой группе испытуемых задали ту же задачу, но вынули содержимое из коробки. Эти испытуемые успешнее решали задачу, видимо, потому, что они с меньшей вероятностью включали в свою репрезентацию функцию коробки как ёмкости и с большей вероятностью учитывали ее функцию как подставки. Исследования, подобные этому и другим, рассмотренным в данном разделе, позволяют понять, почему многие эксперты считают, что хорошая репрезентация задачи — это половина успеха на пути к ее решению. (Этапы решения этой задачи представлены в табл. 9.2.)
Таблица 9.2. Этапы решения задачи
- Представить проблему как высказывание или в визуальной форме.
- Определить цель.
- Разбить цель на подцели.
- Выбрать стратегию решения задачи и использовать ее для решения каждой из подцелей.
Эксперты и новички
В той или иной предметной области (например, физике, географии или шахматах) эксперты решают задачи качественно иным способом, чем новички. Это объясняется различиями в используемых ими репрезентациях и стратегиях. В памяти экспертов может храниться больше конкретных репрезентаций, которые они могут использовать для решения задачи. Мастер по шахматам, например, может посмотреть 5 секунд на сложную комбинацию на доске, включающую 20 фигур, и в точности ее воспроизвести; новичок в той же ситуаций ограничен обычными 7 ± 2 элементами (см. главу 8). Такой трюк с памятью удается экспертам потому, что с годами практики они разработали репрезентации многих возможных позиций на доске; эти репрезентации позволяют им закодировать сложную позицию всего в нескольких единицах. Кроме того, предположительно именно эти репрезентации лежат в основе их превосходства в шахматной игре. Мастер может хранить целых 50 000 конфигураций и знать, что делать в каждой из них. Итак, мастера шахмат могут, по сути, «видеть» возможные ходы; им не надо их выдумывать, как поступают новички (Chase & Simon, 1973; Simon & Gilmartin, 1973).
Даже встречаясь с новой задачей, эксперт представляет ее иначе, чем новичок. Этот момент хорошо проиллюстрирован в исследованиях решения задач в физике. Эксперт (скажем, профессор физики) представляет задачу на языке физических принципов, нужных для ее решения, например: «эта задача относится к типу: всякое действие вызывает равное и противоположно направленное противодействие». Новичок (скажем, студент-физик первого курса), напротив, представляет ту же самую проблему на языке поверхностных свойств, например: «это задача из рода задач с наклонной плоскостью» (Chi, Glaser & Rees, 1982).
Эксперты и новички различаются также используемыми стратегиями. В исследованиях решения физических задач эксперты в общем стараются сформулировать план подхода к задаче, прежде чем выводить уравнения, тогда как новички, как правило, начинают писать уравнения, не имея в голове общего плана (Larkin et al., 1980).
Эксперты решают шахматную задачу качественно иначе, чем новички. Такие эксперты, как мастера игры в шахматы, хранят в своей памяти намного больше специфических репрезентаций, чем они могут применить для решения проблемы.
Еще одно различие состоит в том, что новички работают в противоположном направлении (стратегия движения от цели). Это различие в направлении рассуждения также было выявлено в исследованиях решения задач врачами. Большинство экспертов-врачей рассуждают в прямом направлении - от симптома к возможному заболеванию, тогда как менее опытные их коллеги рассуждают в обратном направлении — от возможного заболевания к симптому (Patel & Groen, 1986).
Рассмотренные характеристики компетентности — множественность репрезентаций; репрезентации, основанные на определенных правилах; планирование перед действием; движение вперед — это некоторые из предметно-ориентированных процедур, которые приходят на смену слабым методам решения задач, рассмотренным ранее.
Влияние мышления на язык
Неужели язык ставит нас в рамки какого-то особого мировоззрения? Согласно самой эффектной формулировке гипотезы языкового детерминизма (Whorf, 1956), грамматика каждого языка представляет собой воплощение метафизики. Например, тогда как в английском есть существительные и глаголы, язык нутка оперирует только глаголами, а язык хопи разделяет реальность на две составляющие: мир явный и мир неявный. Уорф утверждает, что подобные языковые различия формируют у носителей языка образ мышления, непонятный для других. См.→
Как язык может определять мышление: языковая относительность и языковой детерминизм
Никто не спорит с тезисом, что язык и мышление оказывают друг на друга значительное влияние. Однако существуют разногласия по поводу утверждения, что каждый язык по-своему воздействует на мышление и поступки говорящих на нем людей. С одной стороны, каждый, кто выучил два и более языка, поражается тому множеству особенностей, отличающих один язык от другого. С другой стороны, мы предполагаем, что способы восприятия окружающего мира похожи у всех людей. См.→
Решение задачи со свечой